 I had someone ask me about fitting a beta distribution to data drawn from a gamma distribution and how well the distribution would fit. I’m not a “closed form” kinda guy. I’m more of a “numerical simulation” type of fellow. So I whipped up a little R code to illustrate the process then we changed the parameters of the gamma distribution to see how it impacted fit. An exercise like this is what I call building a “toy model” and I think this is invaluable as a method for building intuition and a visceral understanding of data.
Here’s some example code which we played with:
I had someone ask me about fitting a beta distribution to data drawn from a gamma distribution and how well the distribution would fit. I’m not a “closed form” kinda guy. I’m more of a “numerical simulation” type of fellow. So I whipped up a little R code to illustrate the process then we changed the parameters of the gamma distribution to see how it impacted fit. An exercise like this is what I call building a “toy model” and I think this is invaluable as a method for building intuition and a visceral understanding of data.
Here’s some example code which we played with:
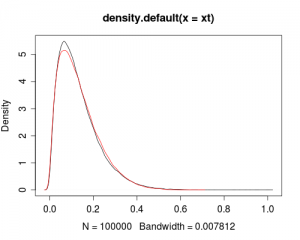
<a href="http://inside-r.org/r-doc/base/set.seed"><span style="color: #003399; font-weight: bold;">set.seed</span></a><span style="color: #009900;">(</span><span style="color: #cc66cc;">3</span><span style="color: #009900;">)</span> x <span style=""><-</span> <a href="http://inside-r.org/r-doc/stats/rgamma"><span style="color: #003399; font-weight: bold;">rgamma</span></a><span style="color: #009900;">(</span>1e5<span style="color: #339933;">,</span> <span style="color: #cc66cc;">2</span><span style="color: #339933;">,</span> <span style="color: #cc66cc;">.2</span><span style="color: #009900;">)</span> <a href="http://inside-r.org/r-doc/graphics/plot"><span style="color: #003399; font-weight: bold;">plot</span></a><span style="color: #009900;">(</span><a href="http://inside-r.org/r-doc/stats/density"><span style="color: #003399; font-weight: bold;">density</span></a><span style="color: #009900;">(</span>x<span style="color: #009900;">)</span><span style="color: #009900;">)</span> <span style="color: #666666; font-style: italic;"># normalize the gamma so it's between 0 & 1</span> <span style="color: #666666; font-style: italic;"># .0001 added because having exactly 1 causes fail</span> xt <span style=""><-</span> x <span style="">/</span> <span style="color: #009900;">(</span> <a href="http://inside-r.org/r-doc/base/max"><span style="color: #003399; font-weight: bold;">max</span></a><span style="color: #009900;">(</span> x <span style="color: #009900;">)</span> <span style="">+</span> <span style="color: #cc66cc;">.0001</span> <span style="color: #009900;">)</span> <span style="color: #666666; font-style: italic;"># fit a beta distribution to xt</span> <a href="http://inside-r.org/r-doc/base/library"><span style="color: #003399; font-weight: bold;">library</span></a><span style="color: #009900;">(</span> <a href="http://inside-r.org/packages/cran/MASS"><span style="">MASS</span></a> <span style="color: #009900;">)</span> fit.beta <span style=""><-</span> <a href="http://inside-r.org/r-doc/MASS/fitdistr"><span style="color: #003399; font-weight: bold;">fitdistr</span></a><span style="color: #009900;">(</span> xt<span style="color: #339933;">,</span> <span style="color: #0000ff;">"beta"</span><span style="color: #339933;">,</span> <a href="http://inside-r.org/r-doc/stats/start"><span style="color: #003399; font-weight: bold;">start</span></a> = <a href="http://inside-r.org/r-doc/base/list"><span style="color: #003399; font-weight: bold;">list</span></a><span style="color: #009900;">(</span> shape1=<span style="color: #cc66cc;">2</span><span style="color: #339933;">,</span> shape2=<span style="color: #cc66cc;">5</span> <span style="color: #009900;">)</span> <span style="color: #009900;">)</span> x.beta <span style=""><-</span> <a href="http://inside-r.org/r-doc/stats/rbeta"><span style="color: #003399; font-weight: bold;">rbeta</span></a><span style="color: #009900;">(</span>1e5<span style="color: #339933;">,</span>fit.beta<span style="">$</span>estimate<span style="color: #009900;">[</span><span style="color: #009900;">[</span><span style="color: #cc66cc;">1</span><span style="color: #009900;">]</span><span style="color: #009900;">]</span><span style="color: #339933;">,</span>fit.beta<span style="">$</span>estimate<span style="color: #009900;">[</span><span style="color: #009900;">[</span><span style="color: #cc66cc;">2</span><span style="color: #009900;">]</span><span style="color: #009900;">]</span><span style="color: #009900;">)</span> <span style="color: #666666; font-style: italic;">## plot the pdfs on top of each other</span> <a href="http://inside-r.org/r-doc/graphics/plot"><span style="color: #003399; font-weight: bold;">plot</span></a><span style="color: #009900;">(</span><a href="http://inside-r.org/r-doc/stats/density"><span style="color: #003399; font-weight: bold;">density</span></a><span style="color: #009900;">(</span>xt<span style="color: #009900;">)</span><span style="color: #009900;">)</span> <a href="http://inside-r.org/r-doc/graphics/lines"><span style="color: #003399; font-weight: bold;">lines</span></a><span style="color: #009900;">(</span><a href="http://inside-r.org/r-doc/stats/density"><span style="color: #003399; font-weight: bold;">density</span></a><span style="color: #009900;">(</span>x.beta<span style="color: #009900;">)</span><span style="color: #339933;">,</span> <a href="http://inside-r.org/r-doc/base/col"><span style="color: #003399; font-weight: bold;">col</span></a>=<span style="color: #0000ff;">"red"</span> <span style="color: #009900;">)</span> <span style="color: #666666; font-style: italic;">## plot the qqplots</span> <a href="http://inside-r.org/r-doc/stats/qqplot"><span style="color: #003399; font-weight: bold;">qqplot</span></a><span style="color: #009900;">(</span>xt<span style="color: #339933;">,</span> x.beta<span style="color: #009900;">)</span>
It’s not illustrated above, but it’s probably useful to transform the simulated data (x.beta) back into pre normalized space by multiplying by max( x ) + .0001 . (I swore I’d never say this but I lied) I’ll leave that as an exercise for the reader.
Another very useful tool in building a mental road map of distributions is the graphical chart of distribution relationships that John Cook introduced me to.